10장 인과와 상관
10.1 인과와 상관
인과 그래프 : 원인과 결과를 원과 화살표로 나타낸 것
인과관계 네트워크 : 인과 그래프의 모음

인과관계의 가치
- 목적을 이루기 위한 구조(메커니즘)에 관한 지식제공
- 인과관계의 이해 == 세상의 구조를 이해
인과관계의 규명은 실험 수행, 통계분석이 필요한 이유이다.
변수 사이의 관계
- 인과관계 : 원인과 결과의 관계 - 원인->결과
- 상관관계 : 데이터에서 보이는 관련성(association)을 말한다.
- 상관에는 한쪽이 커지면 다른 쪽이 커지는(작아지는) 관계인 선형이 대표적이다.
- 일반화된 버전 : 어떤 특정한 조합이 일어나기 쉬우면 : 독립이 아님을 뜻한다.
상관과 인과의 차이
- 관찰 연구를 통해 얻은 데이터를 통해 얻을 수 있는 관계성은 상관.
- 상관을 인과로 보기 힘든 이유
- 중첩요인(confounder: 두 변수에 관련된 외부 변수)가 존재할 가능성
- 역방향 인과관계의 가능성
- 상관을 인과로 보기 힘든 이유
- 인과를 볼 수 있는 방법
- 실험 연구
- 학생에게 원인의 random variable로 무작위로 할당한 후
- 이후에 결과를 조사한다.
- 위는 무작위 통제 실험(randomized control trial,RCT)의 일종
- 인과관계를 간파할 수 있는 이유
- 원인의 조건을 무작위 할당
- 기타 요인의 영향을 제거
- 인과관계를 간파할 수 있는 이유
허위상관(spurious correlation)
- 상관은 있지만 인과는 없을 경우
인과는 있지만, 상관이 없는 경우
주사위를 던지는 행위와 그에 따라 나오는 값

인과관계를 앎으로써 얻는 것
- 변수간의 어떤 메커니즘이 작용하는 지에 대한 이해
- 원인 변수의 어떤 요인이 결과 변수에 어떤 영향을 주는 지에 대한 깊은 이해.
인과관계로 할 수 있는 것
- 개입 : 원인 변수를 변화시킴으로써, 결과 변수를 바꾸기.
- 인과가 없이, 상관만 있는 경우
- 한쪽 변수의 변화가 다른 한쪽 변수의 변화로 이어지지 않는다.
상관관계로 할 수 있는 것
- 상관관계를 통해 인과관계의 존재성을 인지할 수 있음.
- 예측 : 한쪽 변수로부터 또 다른 변수를 알 수 있음.
- 개입의 의미가 아니다.
- 무방향성 : 변수의 방향성이 없기에, 아무 변수로 예측이 가능.
허위상관의 예시
- 아이스크림 매출, 익사 사고 수 : 기온(중첩요인)
- 중첩요인이 되기 쉬운 변수
- 시간또는 나이 : 시간과 함께 증가하는 변수들이 서로 양의 상관을 가지는 경우.
- 중첩요인이 되기 쉬운 변수
- 초콜릿 소비량, 노벨상 : GDP
우연히 생긴 상관 - 정말 아무 연관이 없는 사건의 관계
10.2 무작위 통제 실험
인과관계를 밝히는 방법
인과관계를 밝히기 어려운 이유 : 중첩요인
중첩요인들로 인과를 확인하기 어려운 경우
- 중첩요인 중 나머지는 통제하고 하나를 동일하지 않게 하는 방법
인과 추정 방법
1. 무작위 통제 실험
2. 경향 점수 짝짓기
- 이 방법들은 알고자 하는 요인 이외의 요인은 동일하게 한다는 아이디어가 바탕.
무작위 통제 실험(randomized control trial, RCT)
- 알고자 하는 요인인 변수 X에 표본을 무작위로 할당하고 개입 실험을 수행함.
- 변수 Y와 비교하는 방법
효과
중첩요인을 확인하지 않고도, 효과의 무작위성을 이용하여 알고자 하는 변수의 효과만 추정 가능함.
통계학에서의 인과관계 수식화

할 수 없는 이유
- 한 대상에 개입의 유무를 동시에 볼 수 없기 때문
- 인과 추론의 근본 문제 : 인과효과의 조사는 원리상 불가능하다는 한계
- Sol : 개인 수준인 아닌 집단의 수준으로 생각 -> 인과의 평균적인 효과 고려
- 한계 : 이 경우에도 다이어트를 했을 때와 하지 않았을 때 모두를 관찰할 수 없다.
- 인과 추론의 근본 문제 : 인과효과의 조사는 원리상 불가능하다는 한계

10.3의 한계는
다이어트를 하거나 하지 않았을 때가 아닌
"다이어트하는 집단에 속한 사람"과 "하지 않는 집단에 속한 사람"의 평균값의 차이를 나타낸 것.
이를 해결하기 위해, 조건부 기댓값을 이용한다.

이 공식은 실험 시작 직전에 사람들을 선택하는 과정이다.
선택된 사람들에 대한 평균값을 나타낸 것
이는 다이어트를 하는 사람과 하지 않는 사람의 차이로 비교함으로써 인과효과를 추정할 수 있다.
실험방법 : 이후 시간이 흐른 후에 t검정으로 몸무게 비교
선택편향
정의 : 관측 가능한 개입 효과가 원래 알고자 하는 효과에 편향이 더해질 때, 이 편향을 말한다.
- 다이어트에 의욕이 넘치는 이전에 다이어트를 하지 않았던 사람
10.3 통계적 인과 추론
위의 무작위 통제 실험의 문제점
- 개입 실험의 윤리 문제
- 개입 자체가 불가능한 상황인 경우
담배를 피우라는 강요 : 윤리 문제
담배 가격 : 비용
담배 피우는 사람들 : 큰 표본 구하기의 어려움
이에 대해 통계적 인과 추론으로 대처
- 다중회귀
- 원인변수 : 설명변수x
- 결과변수 : 반응변수 y
- 설명변수 : 중첩요인 z
- 위의 식처럼 bi는 다른 설명변수와의 상관을 제거한 xi의 영향이라고 해석할 수 있는 인과효과를 얻을 수 있다.
- Point : 중첩요인을 측정해 모형에 도입하는 것이 중요.
- 조정 : 중첩요인을 포함하는 것
- 주의점 : 변수의 투입에 따라 인과효과가 달라짐
- 해결안 :
- 도메인 지식이나 선행 연구를 기반하여 상정되는 인과 그래프
- 그래프와 뒷문(backdoor) 기준이라 불리는 기준에 따라 모델 투입 여부 결정
- 해결안 :
뒷문 기준이란? X와 Y 사이의 인과효과를 파악하는데 방해가 되는 경로를 의미한다.
뒷문 기준을 만족하는 것은 (x,y)가 주어졌을 때, x의 자손이 z에 있는 어떤 노드에도 포함되지 않으면서 z가 x로 향하는 모든 경로를 차단할 때 z는 x의 뒷문 기준을 만족한다.
뒷문 기준을 만족하는 조건
1. Z를 막으면 X와 Y 사이의 허위 경로를 모두 막을 수 있다.
2. Z를 막더라도 X와 Y 사이에 직접 연결된 경로는 그대로 남겨두어야 한다.
3. Z를 막았을 때 새로운 허위경로가 생겨서는 안 된다.
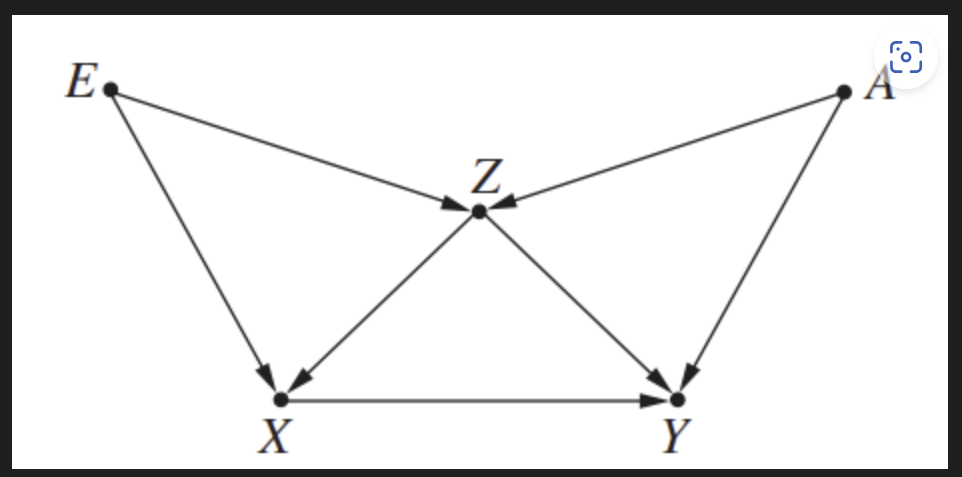
출처: https://blessedby-clt.tistory.com/79 [데이터 탐험 노트:티스토리]
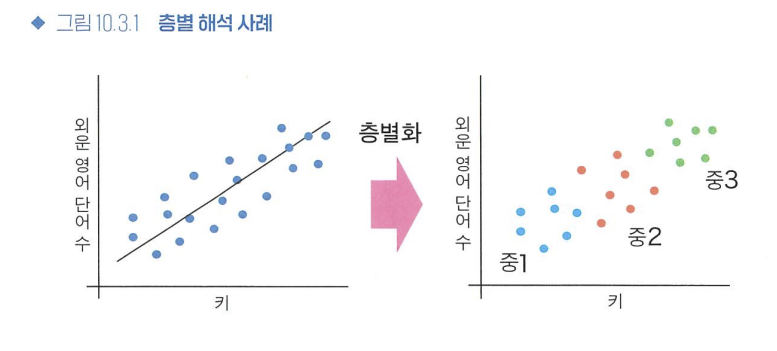
- 층별 해석
- 정의 : 중첩요인을 기준으로 데이터를 몇 가지 그룹(층)으로 나누어, 각 층 안에서 중첩요인의 효과를 가능한 한 작게 하는 방법
- 다중회귀와의 다른 점
- 다중회귀 : 각각 설명변수가 독립으로 인과효과를 갖는다고 가정.
- 층별 해석 : 층마다 다른 인과효과를 추정할 수 있음.
- 주의점
- 층을 구분할 중첩요인을 고를 때 자의적이라는 점
- 중첩요인이 연속인 경우, 이를 이산화하는 방법도 자의적이라는 점
- 다중회귀와의 다른 점
- 정의 : 중첩요인을 기준으로 데이터를 몇 가지 그룹(층)으로 나누어, 각 층 안에서 중첩요인의 효과를 가능한 한 작게 하는 방법
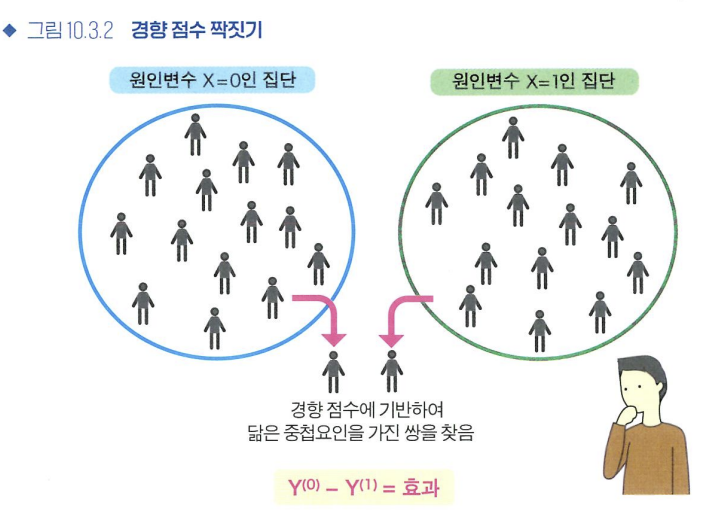
- 경향 점수 짝짓기
- 짝짓기(matching)
- 원인변수=0인 집단과 원인변수=1인 집단에서 비슷한 중첩요인을 가진 데이터를 골라 쌍으로 만드는 짝짓기(matching)라는 방법이 있다.
- 중첩요인 값이 비슷한 데이터들을 짝지으면, 중첩요인 효과를 없애고 무작위 통제 실험과 비슷한 효과를 얻을 수 있다.
- 경향 점수 짝짓기(Propensity Score Matching, PSM)
- 경향 점수라는 1차원 값을 기준으로 쌍을 고르는 방법으로 사용한다.
- 경향 점수 : 원인변수=1인 할당되는 확률
- 순서
- 반응변수를 원인변수(0 or 1)로 한다.
- 중첩요인을 설명변수로 한 로지스틱 회귀를 실행
- "어떤 중첩요인을 원인변수=1에 할당할 지"를 평가
- 장점
- 여러 개의 중첩요인을 동시에 다룰 수 있다는 이점
- 고른 쌍을 통해 반응변수의 차이를 계산하고, 그 평균값을 취해 효과추정량으로 삼는다.
- 짝짓기(matching)
- 이중 차분법
서로 다른 집단 A,B에 대해
A에는 처리를 가하고, B에는 가하지 않은 연구 설계에서
중첩요인에 따라 인과효과의 추정이 어려운 경우
- Sol : 시간 축의 도입, 집단 간 차이에 대해 다시 한번 처리 전후의 차분(차이)을 취함으로써 인과효과를 추정할 수 있다.
- 주의점
- A에 처리를 가하지 않을 경우, B와 같은 정도로 증가한다는, 평행 경향이라는 가정이 필요하다.